Excelシート上で使える、複数の関数を組み合わせた特殊な使い方を説明。
今回は SLOPE、OFFSET、MATCH、COUNTIF、UNIQUE を組み合わせることで、
連続したデータの中から極大点・極小点を探索する方法を紹介。
【本記事の目標】
SLOPE、OFFSET、MATCH、COUNTIF、UNIQUEを使って
極大点・極小点を探索しよう
今回組み合わせる関数は下記でも説明していますので、ご参考ください。

極大点・極小点とは
例えば1日の気温の推移のように、短い間隔でデータを測定していくと、
飛び跳ねたようなデータがなく、ある程度連続してつながったグラフを書くことができます。
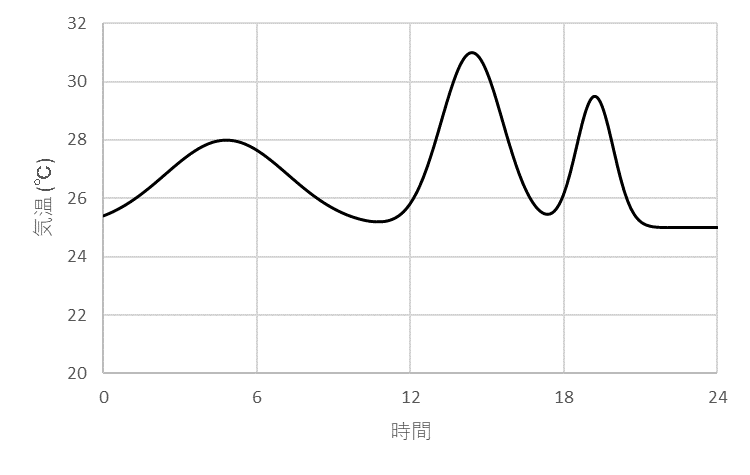
1日の気温の推移が上記のようなグラフのデータになった時、「1日の最高気温・最低気温は何℃ですか?」と聞かれるとこの中のMAX・MINを計算するだけなので、一番高い山・一番低い谷を見ればOKです。
ただそれ以外にも温度が上がったり下がったりして、他にもいくつか山と谷ができていますよね。
この時の山や谷のことを数学用語で【極大】【極小】と言います。
また【極大】【極小】になったときの横軸の値(上記グラフだと「時間」)を【極大点】【極小点】と言い、
その時の縦軸の値(上記グラフだと「気温」)を【極大値】【極小値】と言います。
上記グラフに、
【極大】【極小】、
【極大点】【極小点】、
【極大値】【極小値】
を記載すると、下記のようになります。
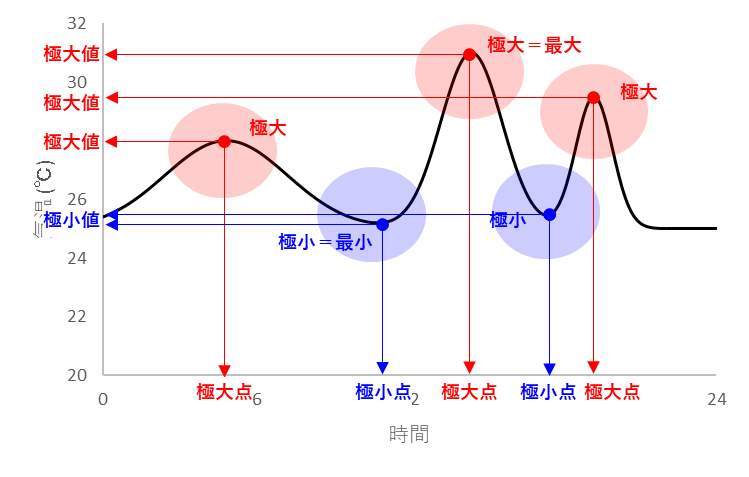
この【極大】【極小】を見ることで、
・午前中に気温が上がって途中で気温が下がったけど、この時間に雨が降ったかな
・昼にまた気温が上がったので、雨が上がって晴れ間が見えたかな
といったことを想像することができます。
上記では気温を例に説明しましたが、それ以外の場面でも、
特にデータの整理や解析をする場合に、この【極大】【極小】に注目することがちょくちょくあります。
グラフに書いてしまえば、【極大】【極小】がどこにあるか問うのは一目瞭然で、
【極大点】【極小点】、【極大値】【極小値】がいくらになるのか、というのもグラフを見ればおおよそ見当を付けることができます。
しかしグラフを書かずに、Excel関数を駆使して【極大点】【極小点】、【極大値】【極小値】を求めるには、少し複雑な手段をとる必要があります。
今回はそのExcel関数を駆使して【極大点】【極小点】、【極大値】【極小値】を求める方法について解説していきます。

極大点・極小点の計算手順
Excel関数を駆使して【極大】【極小】を計算する方法は、大きく分けると3つのステップに分かれます。
1.グラフの傾きを計算・確認する
2.極大・極小では傾きが0になるので、傾きが0になっているポイントを探す
3.傾きが0になっているポイントをリスト化して並べ、その時の縦軸の値を取ってくる
それぞれの手順について詳しく説明していきます。
手順① 傾きを確認する(微分)
まずはグラフの傾きを確認していきます。
【極大】【極小】のポイントでは傾きが0の水平の状態になりますので、傾きを見れば【極大】【極小】を見つけることができます。
(この傾きを計算することを、数学用語で『微分する』と言います。)
Excelで傾きを計算するのは非常に簡単で、SLOPE関数を使って計算すればOKです。
ただし、SLOPE関数で指定する「既知のy」「既知のx」にはできる限り狭い範囲を指定します。
そうすることで、その狭い範囲での傾きを見ることができます。
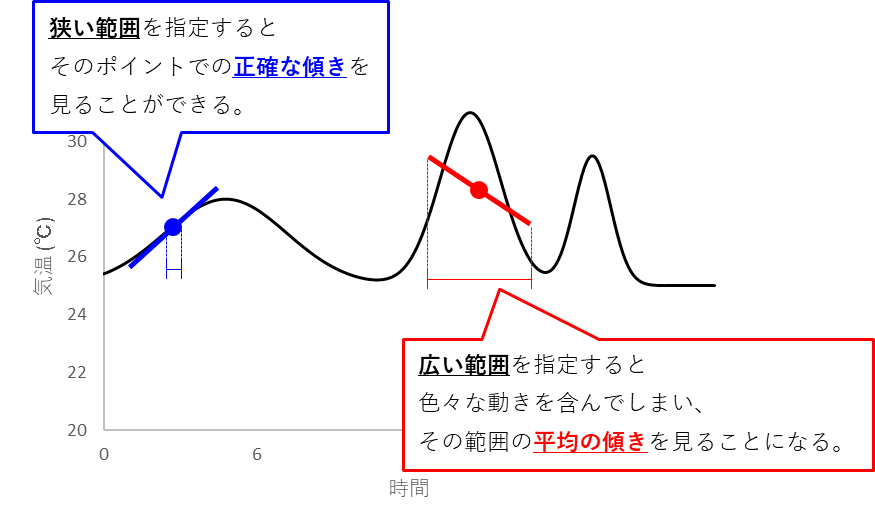
実際にExcelで計算する場合、
A列にグラフの横軸のデータ、B列にグラフの縦軸のデータがあるとすると、
あるポイントでの傾きは、そのポイントのデータの前後1つ程度を指定してSLOPE関数を入力します。
この関数を全てのデータについて計算していきます(関数を最後の行までコピーします)。
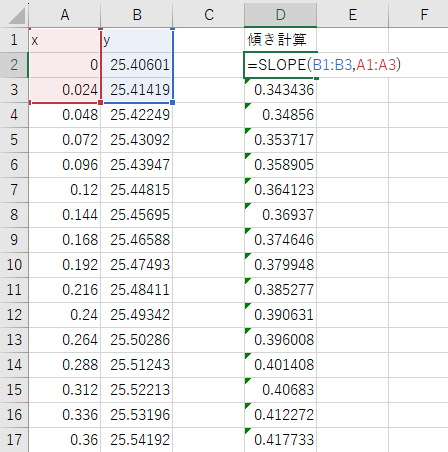
ここではデータの前後1つのデータ範囲を指定していますが、必ずしもこの範囲で指定しないといけない、というわけではないです。
データによっては細かなノイズが入っていてガタついている場合もあるため、少し広めに範囲を指定した方が良い場合もあります。
そういった場合に、後で自由に指定する範囲を変更できるように、データ範囲をOFFSET関数を使って指定しておくことをオススメします。
=SLOPE(OFFSET(B2,-$E$1,0,$E$12+1,1),
OFFSET(A2,-$E$1,0,$E$12+1,1))
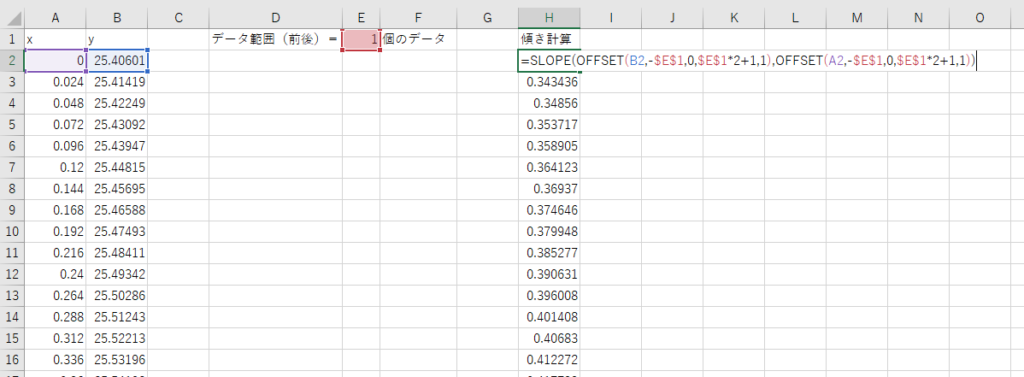
関数としてはかなり複雑になりますが、後々のことを考えると自由度は高くなります。
手順② 傾きが0になるポイントを探し出す
手順①で傾きを計算することが出来ましたので、この中から傾きが0になっているポイントを探し出します。
値が0になっている部分を探す関数として、MATCH関数やVLOOKUP関数等がありますが、これらの関数は
・近い値を探す場合は、データが昇順もしくは降順に並んでいる必要がある
・データが昇順もしくは降順に並んでいない場合は、「完全一致」で探す必要がある
という制約があるため、ここでは使うのが困難です。
そのため違う方法で値が0になる部分を探す必要があります。
絶対値(ABS)を使って値が0のポイントを特徴的なポイントに変える
上記のグラフに傾きのグラフを重ねると下記のようになります。
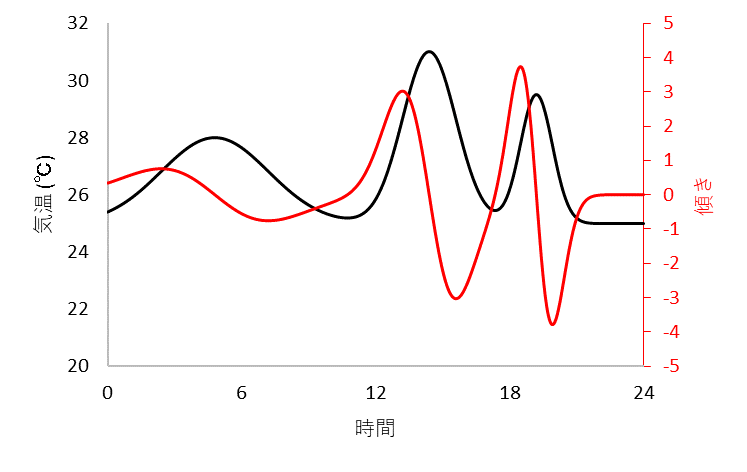
これだと傾きが0の部分を目視で探そうとしてもちょっと分かりづらいですよね。
なぜ分かりにくいかというと、傾きはマイナスになる場合もあるので、傾きが0の部分というのがグラフの中心部分に来てしまっているせいです。
「じゃあ、傾きが全部プラスの値になれば、
傾きが0の部分は特徴的な形になるかも!」
実際にグラフにしてみましょう。
マイナスのデータを全てプラスに変えてしまうには、
絶対値(ABS関数)を使うことでできます。
ABS関数は、絶対値を表示したい値を指定するだけで使用できる非常に簡単な関数です。
=ABS(絶対値を表示したい値)
実際に先ほど計算した傾きの絶対値を計算してグラフを書くと、下記のようになります。
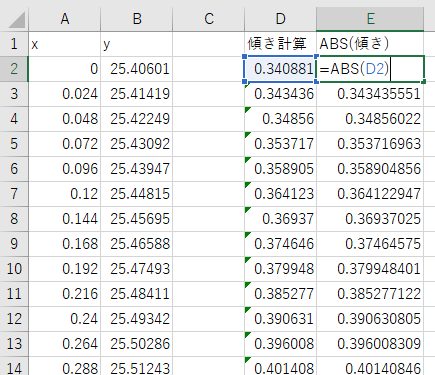
↓
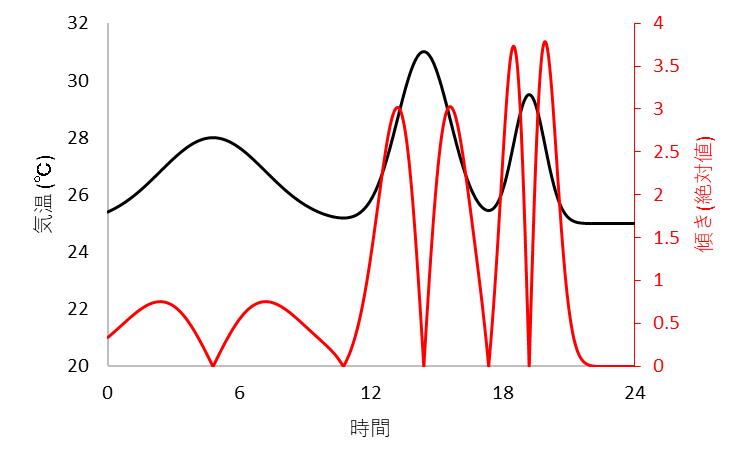
先ほどのグラフと変わって、傾きが0の部分が一番下に来て、
かつ尖った形になっているので、目視でも見つけやすくなりましたね。

一定の幅の中での最小値(MIN)を計算し、傾き0の部分を際立たせる
絶対値に変えることで、傾きが0の部分というのがその周辺のデータの中で必ず最小値になるようになりました。
「じゃあ、適当な範囲の最小値(MIN)がどこにあるかを、
MATCH関数を使って探し出したら傾きが0の部分を探し出せるかも!」
ということで、実際にやってみます。
適当な範囲として、一旦前後10個分のデータ(計21個)を使ってその中の最小値を計算します。
最初の方のデータは前10個分のデータが無いためエラーが出てきますが、とりあえず無視して計算します。
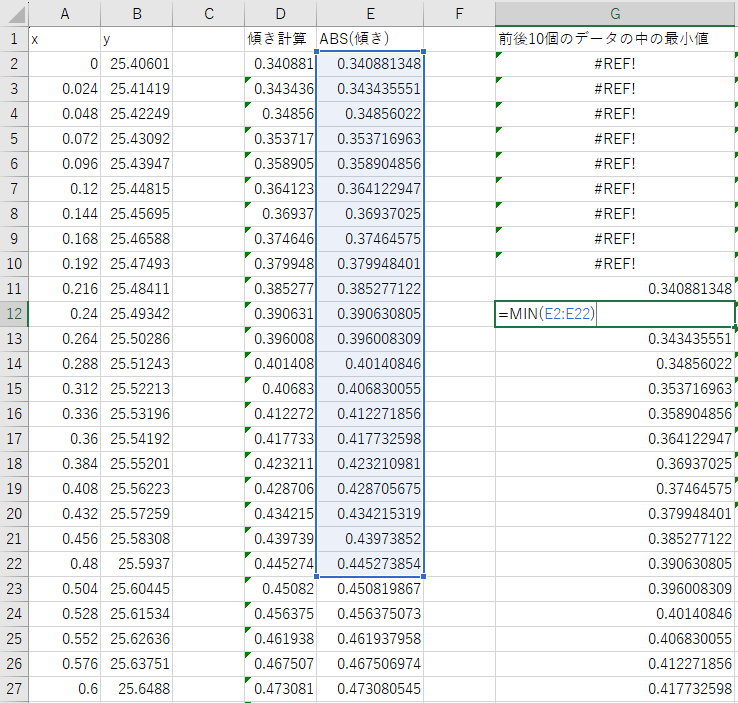
この最小値がE列の上から何個目にあり、その時のxの値がいくつかを計算したいので、
OFFSET関数+MATCH関数を使って計算します。
OFFSET関数+MATCH関数の使い方は下記でも説明していますので、ご参考ください。
実際に計算式を入力すると、下記のようになります。
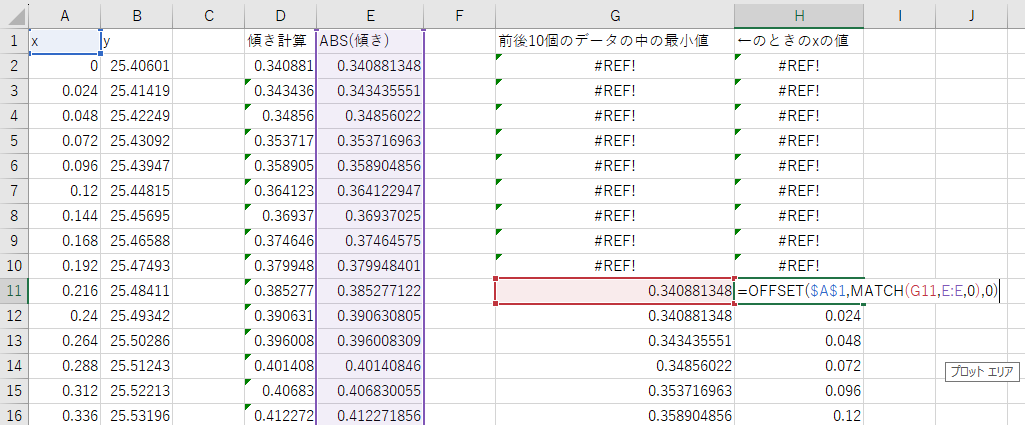
この計算をすると、パッと見はA列のデータがそのまま表示されているようにしか見えないかと思います。
ただ、ABS(傾き)の部分が0になっている部分のデータを見てみると明らかに違う動きをしています。
↓
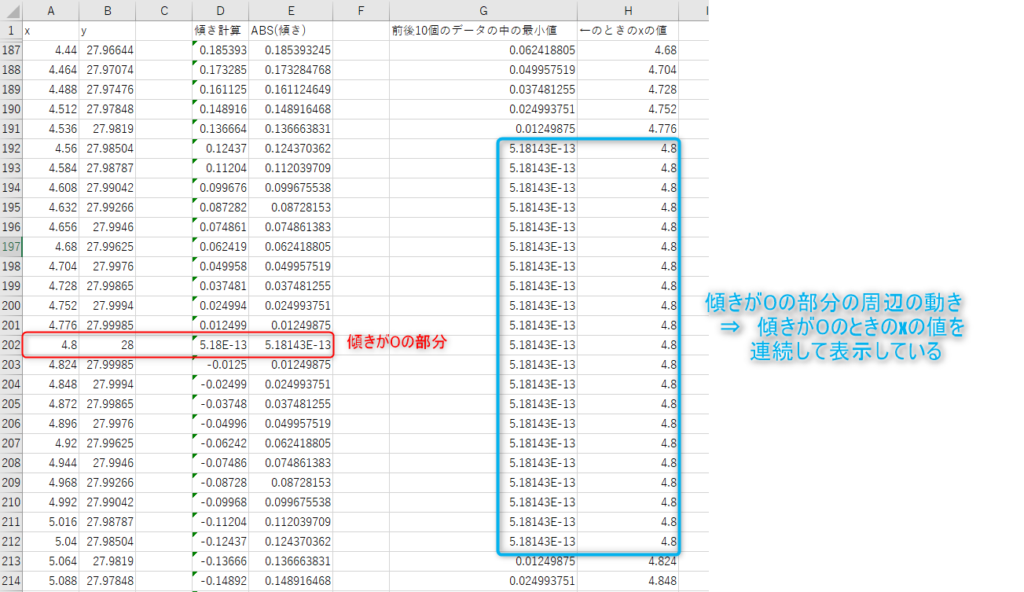
このようにMIN関数・OFFSET関数・MATCH関数を使うことで、傾きが0の周辺部分で
「傾きが0の部分はここですよ!!」
と主張しているような結果にすることが出来ました。
連続して表示されている部分をCOUNTIF関数を使って確認
上記の関数を入力することで、傾きが0になっているポイントのxの値が連続して表示されるようになりました。
あとは、COUNTIF関数とIF関数を使って、
・この値は何回表示されているのか
・その回数が一定以上の場合はその値を表示させ、それ以外は空欄にする
という関数を記入してあげると、連続して表示されている傾きが0のポイントだけが残るようになります。
実際に入力すると下記のようになります。
(今回は表示されている回数が5回以上のデータだけ残すようにしています。
回数についてはMIN関数で指定したデータ数以下であればOKです。)
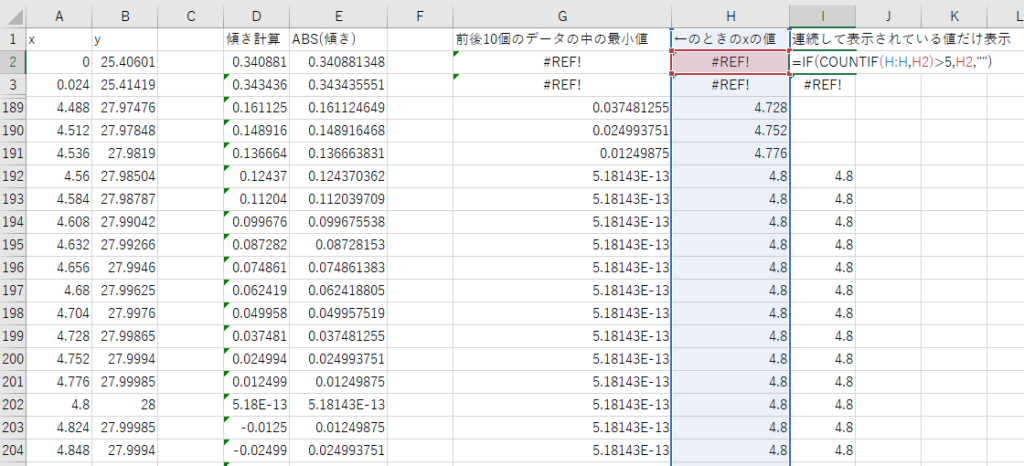
ここまでの関数を入力していくと、I列には傾きが0のポイントのxの値だけが表示されるようになっているはずです。
ここまでに入力した関数の一覧
一気にたくさんの関数を入力したので、一旦ことで入力した関数の一覧を書き出しておきます。
2行目だとエラーが出ているので、20行目に入力されている関数を書き出しておきます。
この関数を、全ての行にコピーしておけばOKです。
E列: =ABS(D20)
G列: =MIN(E10:E30)
H列: =OFFSET($A$1,MATCH(G20,E:E,0),0)
I列: =IF(COUNTIF(H:H,H20)>5,H20,””)

手順③ 傾きが0になったポイントのリストを書き出す
上記までの関数を入力することで、I列には傾きが0のポイントのxの値だけが表示されているはずです。
ただ、I列に表示されているだけでは使いづらいので、
I列に表示されたデータの重複を削除して結果のリストとして表示してほしいですよね。
ここで使うのがUNIQUE関数です。
UNIQUE関数を使ってI列に表示されているデータの重複を削除してリストを表示させてみましょう。
すると結果が下記のようになります。
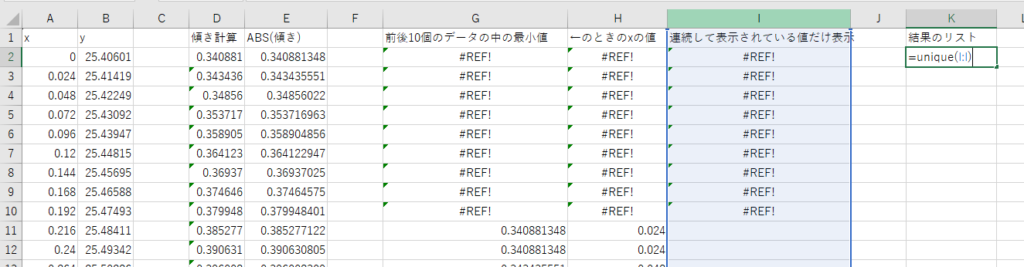
↓
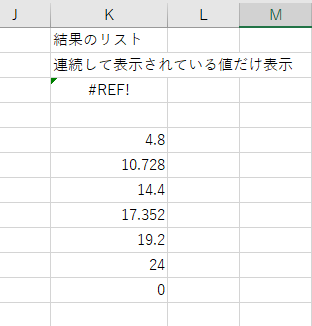
1行目に記載しているタイトルや、エラー表示の「#REF!」も表示されていますが、
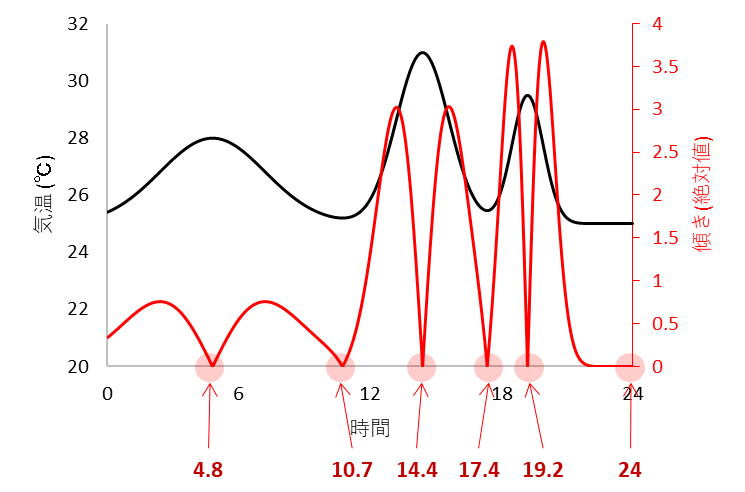
それ以降の 4.8 ~ 0 の値が、【極大点】【極小点】になります。
実際にグラフで確認してみても、この点が【極大】【極小】になっているのが確認できます。
【極大点】【極小点】が分かれば、
【極大値】【極小値】はOFFSET関数+MATCH関数を使えば求めることが出来ます。
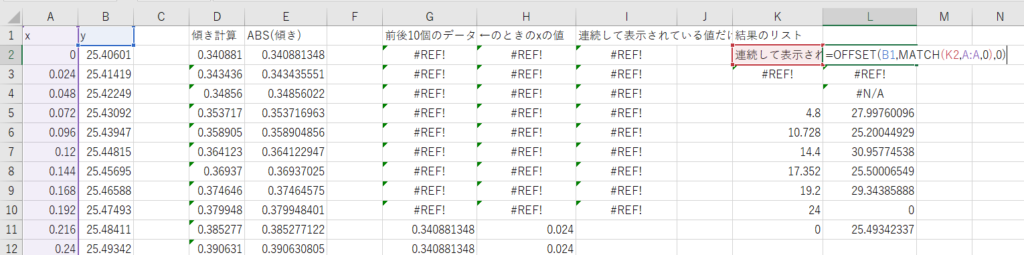
まとめ・計算結果
今回記載した関数を下記に書き出しておきます。
(D列~I列は20行目のデータ)
D列: =SLOPE(B19:B21,A19:A21)
E列: =ABS(D20)
G列: =MIN(E10:E30)
H列: =OFFSET($A$1,MATCH(G20,E:E,0),0)
I列: =IF(COUNTIF(H:H,H20)>5,H20,””)
極大点・極小点のリスト: =UNIQUE(I:I)
極大値・極小値のリスト: =OFFSET(B1,MATCH(K2,A:A,0),0)
(極大値・極小値は、UNIQUE関数のスピルの結果部分と同じ行までコピーが必要)
この計算をすることで、今回のデータの場合、下記のようなリストを得ることが出来ます。
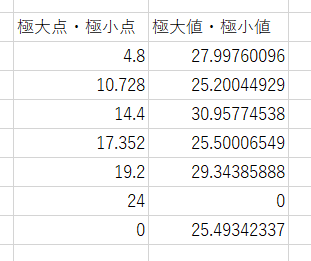
極大・極小は必ず交互に出てきますので、極大値・極小値のデータが
1つ前よりも高いと極大
1つ前よりも低いと極小
になります。

SLOPE関数の部分でも少し触れましたが、データ範囲を指定する関数の部分は、後々自由に範囲を操作できるようにOFFSET関数を使って範囲を指定しておいた方が良いです。
OFFSET関数を使った場合、入力する関数は下記のようになります。
(全て2行目に入力している関数です)
D列: =SLOPE(OFFSET(B2,-$E$1,0,$E$12+1,1),
OFFSET(A2,-$E$1,0,$E$12+1,1))
E列: =ABS(H2)
G列: =MIN(OFFSET(I2,-$E$2,0,$E$2*2+1))
H列: =OFFSET($A$1,MATCH(K2,I:I,0),0)
I列: =IF(COUNTIF(L:L,L2)>$E$3,L2,””)
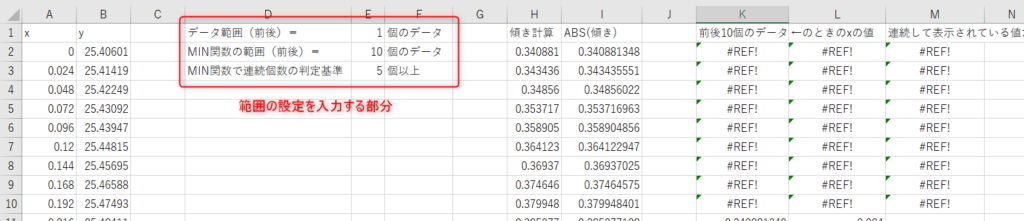
かなり複雑になりますが、OFFSET関数を使わない場合の関数を知っていれば理解できるかと思います。
こういった形で関数を入力できるようになると、関数の修正等が簡単にできるようになっていきますので、頑張って慣れていきましょう。








コメント