最近、様々なメディアやSNSで投資について解説されています。
また2024年には新NISAも始まり、国も国民に投資をすることを勧めているように感じます。
投資と言っても様々なものがありますが、特に注目されているのが
投資信託
です。
この【投資信託】が注目されているのは様々な理由がありますが、その中の1つに
『S&P500』という指標に連動するインデックス投資で、15年以上積み立てた場合、
1960年以降のどの15年間を切り取っても平均年利が4~5%以上を実現
という勝ち確定の歴史をたどってきた、という点が挙げられます。
ただ、これだけ聞いても
平均年利4~5%以上って何がどうすごいの?
となると思います。
投資信託の一番のメリットは、この「年利4~5%」というのが【複利】で効いてくるからなのですが、それだけ聞いてもよくわからないですよね。
ただそれだけで、
投資信託なんてよくわからないからやらない~
というのは非常に、ひじょ~にもったいない!
なので、まずは「投資信託って何?」ということに興味を持っていただくため、
【複利】でこんなにお金が増えていくんだ♪
という点を、実際に自分で計算して体感してもらえたらと思います。
【本記事の目標】
【複利】の計算をして、その効果の大きさを体感しよう

そもそも金利って?
金利とは?
そもそも【金利】って何?
金利というのは簡単に言うと、
ある商品を一定期間持っているだけで、一定期間後にその商品の価値の○%分を
商品価値に上乗せされる。この時の○%が金利
と言い換えることが出来ます。
ここで言う『商品』というのが、
【株】や【投資信託】や【不動産】、
もしくは【カードローン】や【住宅ローン】や【借金】
になるわけです。
| 株 | 毎年(年に1~4回)、配当金として持ち株数に応じた金額を受け取る |
| 投資信託 | 毎年、分配金として投資額に応じた金額を受け取る(再投資も可能) |
| 不動産 | 毎月、家賃収入として入居者から家賃を受け取る |
| ローン | 毎年、借入額に応じた金額(利息)だけ借入額が増える |
| 借金 | 一定期間ごとに、借入額に応じた金額(利息)だけ借入額が増える |
金利はいつ適用されるの?
金利の説明に『一定期間』と記載しましたが、この『一定期間』というのはその商品によって様々です。
ただ、多くの商品(株、投資信託、住宅ローン等)は1年間というのを1つの区切りにしており、例えば金利5%であれば1年後には商品の価値の5%が受け取れます。
(※住宅ローンの場合はローンが5%増えます)
このように1年間を区切りとしている金利を特別に【年利】と言います。
この金利というのは、一定期間を過ぎたら一度だけ適用されるわけではなく、
一定期間ごとに何度も適用されます。
金利は一定期間ごとに何度も適用されるため、
金利が何度も適用された状態のことを【複利】と言います。
複利のすごさって?
この【複利】が、投資の世界で最も重要と言っても過言ではないぐらい重要なキーワードです。
例えば、
ある株に100万円投資を投資しました。
この株の配当金は年利で5%です。
この配当金を使って同じ株を買い続けたとき、10年後にいくらの株を持っているでしょう?
という場合、どういう計算になるでしょうか。
100万円の5%は5万円ですので、1年後には5万円を受け取れます。
これが10年繰り返されるので、
100+5+5+5+5+5+5+5+5+5+5=150
ということで150万円! というとそうではないです。
100万円の5%は5万円ですので、1年後には5万円を受け取れます。
この5万円で再度同じ株を購入していますので、
2年後には105万円に5%の金利がかかり、配当金は5.25万円になります。
これが10年繰り返されると、、、最終的には163万円!
単純に足し算されたときに比べ、13万円も多くなります。
これが複利の効果です。
ここではいきなり答えを出しましたが、この計算はExcelを使えば簡単にできます。
(手計算でもできなくないですが、ちょっと大変です)
そこで、実際にExcelの計算シートを作ってみて、
今の貯金額100万円を年利5%の投資信託に投資したら20年後どんな額になるんだろう?
子供の出産祝いの30万を年利5%の投資信託に投資しておいたら、
子供が定年後にはどんな額になっているんだろう?
といった計算をして、複利の効果のすごさを体感してもらえたらと思います。
Excelシートを使って実際に複利を計算
最終的なExcelシートの構成
今回作る【複利計算のExcelシート】は下記のイメージで作っていこうと思います。
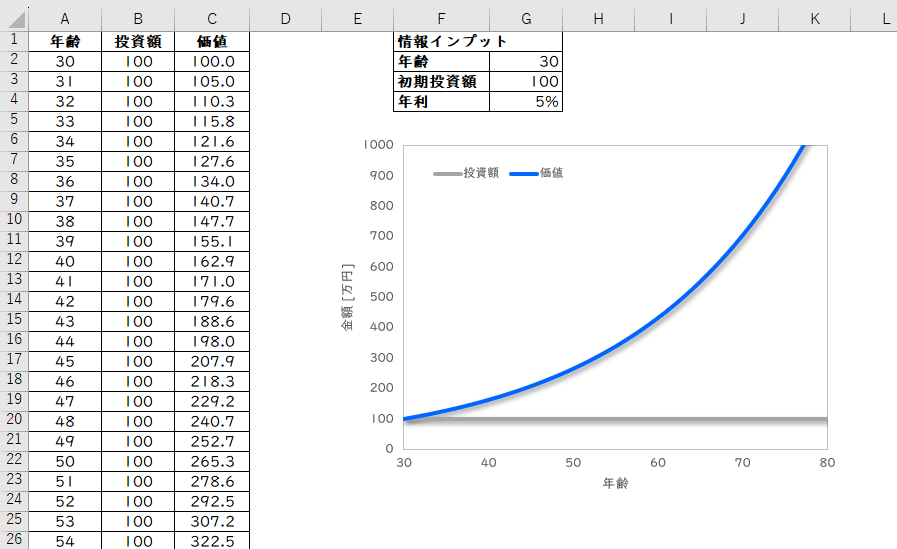
基本の数値を入力
まずは計算したい基本情報を入力する部分を作ります。

今回の計算では
- 年齢(自身の現在の年齢)
- 初期投資額(最初に投資する金額)
- 投資した商品の年利
を記入し、その情報で計算をしていきます。
この部分はただの情報記入欄ですので、上記3点が記入できるように欄を作っておきます。
今回は単純化のため、最初に投資して以降は投資しない設定で計算式を作っています。
ただ実際の投資では、リスク分散のため少額でも良いので定期的に積み立てていく方法(ドルコスト平均法)が推奨されています。
この方法を計算する場合は計算式が若干複雑になりますので、
ドルコスト平均法での計算については、次回説明したいと思います。
計算式を入力
計算式が記入されているのは左側の、A列、B列、C列、です。
また計算式は、2行目、3行目以降で分かれていますので、それぞれ説明していきます。
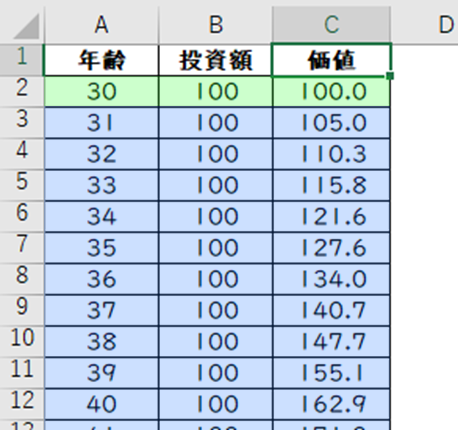
A列2行目:最初の年齢
A列には年齢を記入していきます。
A列の2行目は、計算を開始する時点での年齢ですので、”G2”セルに記入してある年齢をそのまま持ってきます。
=G2
B列2行目:最初の投資額
B列には実際に投資した額(支払った額)を記入していきます。
B列2行目は最初の投資金額ですので、”G3”セルに記入してある投資金額をそのまま持ってきます。
=G3
C列2行目:最初の投資額の価値
C列には投資した額がどんな価値になっていくかを記入していきます。
C列2行目は最初の時点ですので、まだ金利も無いため投資額がそのまま価値になります。
=B2
A列3行目以降:年齢
A列には年齢を記入していきます。
年齢は1年ごとに1歳追加していけばOKですので、1つ上のセルに+1をすればOKです。
=A2+1
上記の式を”A3”セルに記入して、それを下にコピーしていきます。
(今回は50セル下までコピーしました)
B列3行目以降:投資額
B列には実際に投資した額(支払った額)を記入していきますが、
今回は最初に投資した以降は投資していかない(配当金だけ投資していく)ため、
”B2”セルの値がそのまま変わらないです。
=B2
(上記の式を”B3”セルに記入して、それを下にコピーしていきます。)
C列3行目以降:投資額の変化
C列には投資した額がどんな価値になっていくかを記入していきます。
投資した額の価値は、1年後には 前年の価値×(1+年利) になるので、
=C2*(1+$G$4)
となります。
上記の式を”C3”セルに記入して、それを下にコピーしていきます。
計算式をコピーしていくと、G4セルを参照している部分が変わってしまうため、
コピーしても変わらないように絶対参照(「$」を付ける)にしています。
絶対参照については下記記事もご参考ください。
今回は分かりやすくするため、2行目と3行目以降で計算式を分けて紹介しました。
ただこの場合、間違えて2行目の計算式を全ての行にコピーしてしまうと、3行目以降の計算式が消えてしまい、計算が出来なくなってしまいます。
それを避けようと思うと、2行目以降全てに同じ式を適用させる必要があります。
この場合の計算式も下記に記載しておきます。
若干分かりにくいですが、1つずつ分解していくと理解できるかと思います。
■A列2行目以降
=$G$2+ROW()-ROW($A$2)
■B列2行目以降
=$G$3
■C列2行目以降
=IF(ROW()=ROW($C$2),G3,C1*(1+$G$4))
グラフを追加する
上記までで計算式の入力は完了です。
後は基本情報の入力欄に好きな数値を入力してみて、
自身の年齢が何歳の時に、投資した額がどのぐらいの価値に増えているのかを見ていけばOKです。
ただせっかくなので、数値だけで見ていくよりもグラフにしてしまって、
複利のすごさをより分かりやすくしてみましょう。
グラフ化する際は、A~C列を選択して『散布図』のグラフを挿入します。
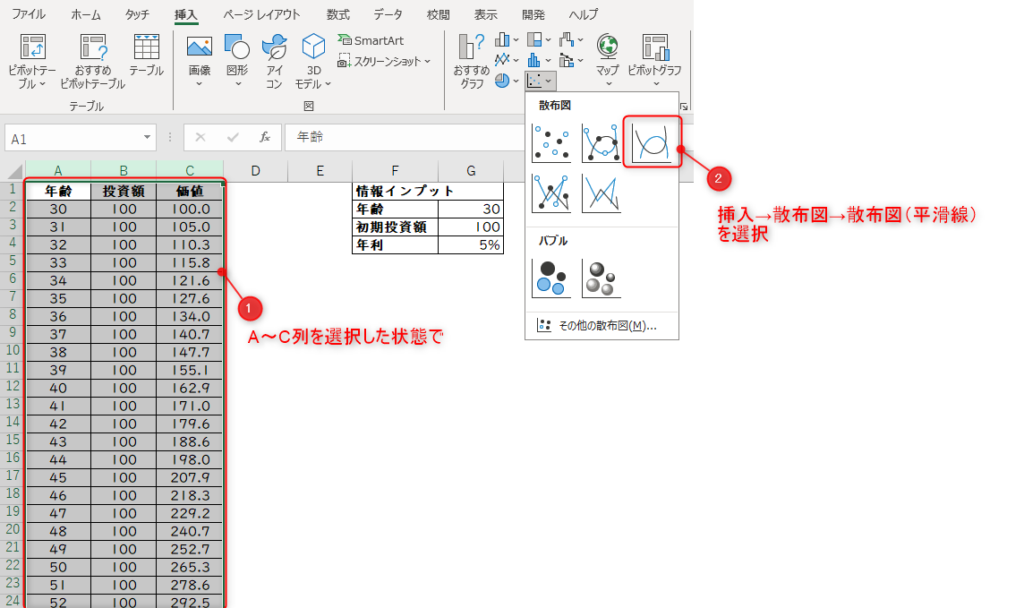
挿入されたグラフには、
① 投資額
② 価値
の2つの線があると思いますが、この線の差分が投資によって増えた金額になります。
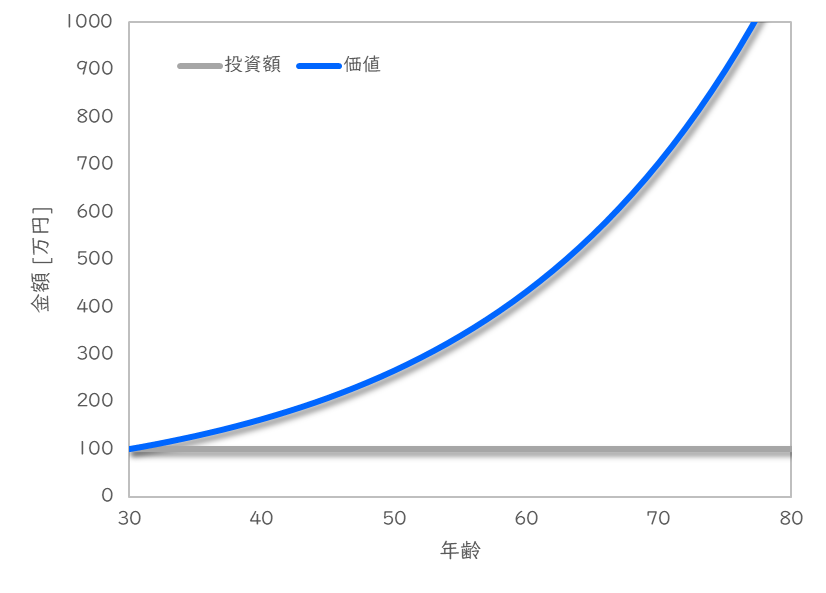
(このグラフは書式を色々変更しています。
自身のシートでも見やすいように変更していただいてOKです。)
実際に計算してみて効果を体感
計算用のシートは上記で完成です。
では実際にいくつかのケースを計算してみて、複利の効果を体感してみましょう。
ケース1:30歳で200万を投資、年利5%で退職時(60歳)まで運用
この場合の推移は下記のようになります。
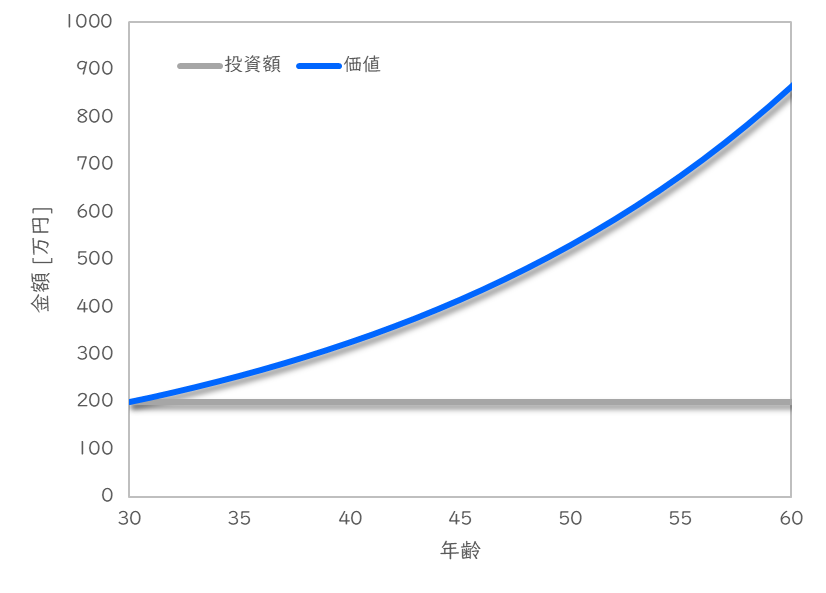
30歳で投資した200万円が、30年後の60歳時点では864万円になります。
30年かけると4倍にまで膨れ上がります。
(配当金は全て再投資した想定)
ケース2:20歳で100万を投資、年利4%で70歳まで運用
この場合の推移は下記のようになります。
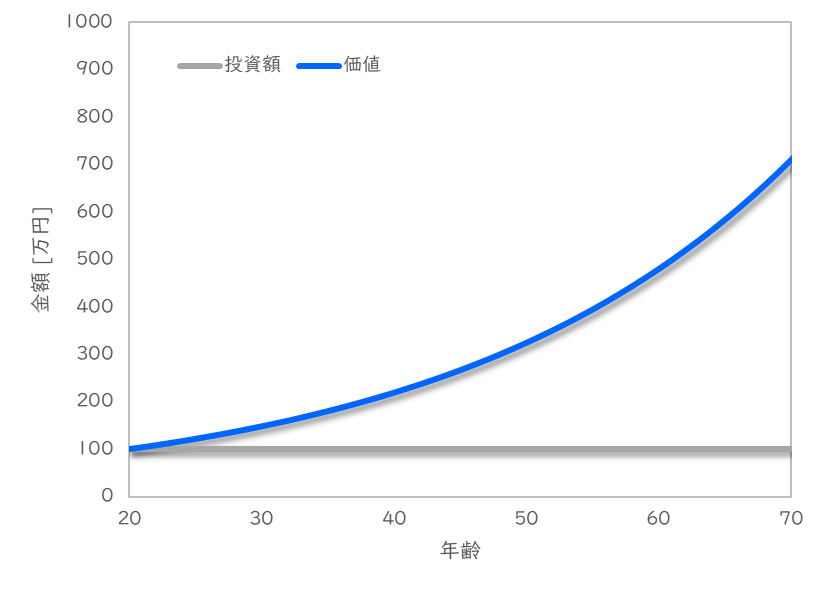
20歳の時に何とか100万円を捻出して、比較的現実的な年利4%で運用すれば、
70歳時点では710万円になっており、実に7倍に膨らみます。
ケース3:子どもの出産祝いの30万円を投資、 年利4%で子どもが70歳まで運用
この場合の推移は下記のようになります。
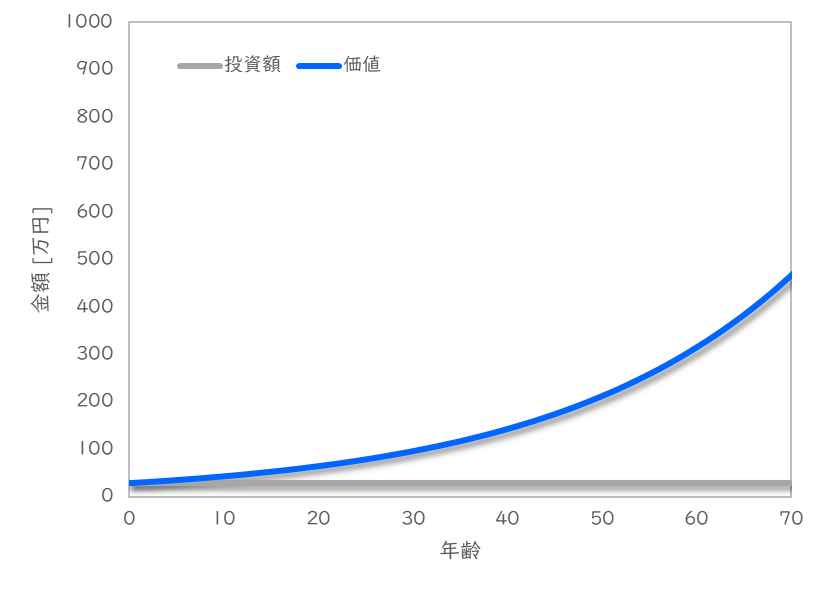
初期に投資している金額が大きくないためあまり増えているように感じないかもしれませんが、
70歳時点では467万円になっており、倍率でいくと実に15倍に膨らんでいます。
複利の効果のすごさについて
上記のケース以外にも、ご自身の状況にあったケースで計算してみていただけると、
複利のすごさを実感していただけると思います。
ただ、実際に計算してもらうと分かりますが、
複利のすごさは長期間投資して初めて発揮されます。
もちろん投資する金額が高いほど効果は大きいですが、
どんな金額を投資したとしても、同じ期間投資すれば、倍率は同じになります。
(100万円投資しても、1万円投資しても、年利5%であれば30年後に4倍に増えます)
ですので、
いくらを投資するか?
についてはあまり気にせずに
いつから投資するか?
を気にして、少額でも良いから始めた方が、より大きなメリットを受けられます。



コメント